Myślenie komputacyjne to jedno z ważniejszych podejść do rozwiązywania problemów. Jest zestawem postaw i umiejętności, wzorców myślenia oraz procesów przydatnych przy rozwiązywaniu problemów. Składa się na nie kilka metod rozumowania (ang. mental tools), między innymi: myślenie logiczne, abstrakcyjne, uogólnianie, budowanie algorytmów. Myślenie komputacyjne wyrosło na gruncie informatyki, ale przydaje się w innych dziedzinach, w rozważaniu sytuacji problemowych.

Chciałbym w tym artykule przybliżyć Państwu, jak myślą dzieci, gdy stają przed wyzwaniem znalezienia rozwiązania łamigłówki. Łamigłówki dobierzemy rozmyślnie, by podczas ich rozwiązywania zastosować naturalne sposoby rozumowania (ang. mental tools), które złożą się na myślenie komputacyjne, będące obecnie naczelnym podejściem do rozwiązywania różnorodnych problemów. Chociaż to pojęcie wyrosło na gruncie informatyki, może być przydatne w rozważaniu różnorodnych sytuacji problemowych.
Dobrym przykładem są popularne łamigłówki Sudoku. Swoje rozważania ilustruję interaktywnymi aplikacjami z pakietu Informatyka dla Smyka, dostępnego na platformie Dzwonek.pl. Proponuję, by Czytelnik w trakcie rozważań wczuł się w rolę dziecka i nie tylko sam rozwiązywał łamigłówkę, ale jednocześnie omawiał każdy kolejny ruch i go uzasadniał.
Zacznę od uproszczonych wersji Sudoku, znanych jako kwadraty łacińskie. Na ilustracji poniżej przedstawione są dwie najprostsze łamigłówki z modułu Sudoku I. Częściowo są wypełnione i prosimy dzieci, by wypełniły je tak, aby w każdej linii (wierszu i kolumnie) znalazły się owoce każdego rodzaju (lewy diagram) lub każdy rodzaj szkolnego przyboru (prawy diagram). Można wielokrotnie się przymierzać, zmieniać i wycofywać ruchy oraz rozpoczynać od początku. Nauczyciel powinien wiedzieć – dla swojego komfortu – że każda taka łamigłówka ma rozwiązanie (to fakt matematyczny).
Podobne łamigłówki można utworzyć bez komputera, na przykład na podłodze, stole lub jakiejś podkładce i wypełniać je przygotowanymi zawczasu obrazkami figur geometrycznych, nazbieranymi przez dzieci liśćmi, nakrętkami z butelek itp. Kwadraty mogą mieć różną wielkość, jak poniżej. Zauważmy, że posługując się aplikacją Informatyka dla Smyka, komputer pośredniczy jedynie w prezentacji i pod żadnym względem nie ułatwia rozwiązywania tych łamigłówek, ułatwia jedynie wielokrotne ponawianie prób.


Z mojego doświadczenia wynika, że nawet starszym dzieciom z przedszkola i uczniom w pierwszej klasie wypełnienie powyższych łamigłówek nie sprawia kłopotu.
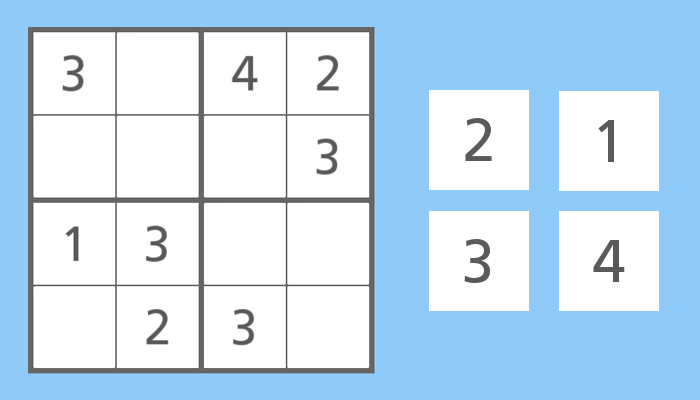
Na kolejnej ilustracji przedstawione jest Sudoku ze zwierzętami w układzie zbliżonym do klasycznego – różne mają być zwierzęta w wierszach, kolumnach i kwadratach 2×2. Po prawej stronie znajduje się Sudoku z cyframi w miejscu zwierząt. Zauważono, że ta „analogowa” wersja jest znacznie wolniej rozwiązywana przez dzieci niż ta cyfrowa.

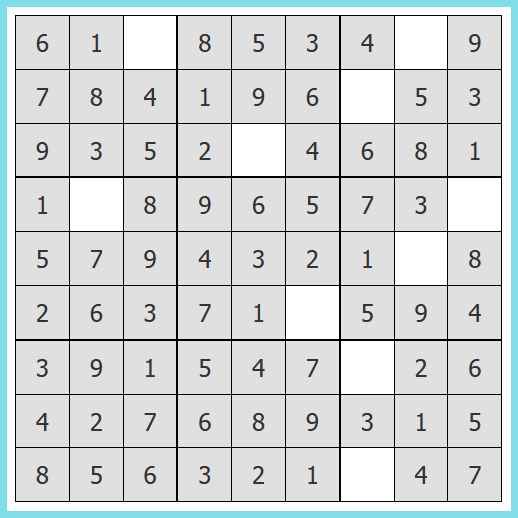
Na koniec tej zabawy można poprosić dzieci o wypełnienie oryginalnego Sudoku 9×9 – dzieci poznają cyfry (liczby) w zakresie od 1 do 10 już w pierwszej klasie. To łatwiejsza wersja – wystarczy decydować na podstawie pojedynczych fragmentów (wierszy, kolumn, kwadratów). W modułach Sudoku II i III w pakiecie Informatyka dla Smyka zamieszczone zostały nieco trudniejsze łamigłówki.
Rozmowa z dziećmi uzmysłowiła mi, że stosują następującą zasadę:
Zasada. W pustym miejscu można umieścić wybrany obiekt (owoc, przyrząd, zwierzątko, cyfrę), jeśli brakuje go we wszystkich fragmentach planszy, do których należy to puste miejsce, takich jak wiersz, kolumna lub kwadrat. A zatem w tym pustym miejscu nie można umieścić żadnego innego owocu, przyrządu, zwierzątka, cyfry, jeśli już się znajduje w wybranym fragmencie, takim jak wiersz, kolumna lub kwadrat.
Prześledźmy możliwy sposób rozwiązania Sudoku ze zwierzątkami. W kwadracie po prawej u góry wstawiana jest brakująca w tym kwadracie owca, a w kwadracie u dołu po lewej – brakujący pies, bo brakuje ich w tych kwadratach. Po tych decyzjach, drugi wiersz możemy uzupełnić psem, a czwarty – owcą, bo ich tam brakuje. Na końcu, w dowolnej kolejności można wypełnić pojedyncze puste pola w każdej kolumnie. Zastosowaliśmy Zasadę do pojedynczych fragmentów planszy, najpierw kwadratów, później wierszy i na końcu kolumn. Możliwe są inne sposoby (kolejności) wypełnienia tego Sudoku.
Zinterpretujmy teraz podejmowane decyzje. Przyjmijmy za wzorzec dla kolejnych kroków postępowania i podejmowania decyzji fragment planszy z jednym niewypełnionym miejscem – takie miejsce można natychmiast wypełnić jedynym możliwym obiektem.
- w poszukiwaniu wzorca dzieci rozkładają (dekomponują) planszę na mniejsze fragmenty: wiersze, kolumny, kwadraty, w których uzupełniają rozwiązanie;
- wielokrotne wykonanie kroku (1) prowadzące do pełnego rozwiązania składa się na algorytm rozwiązania łamigłówki, ten algorytm ma bardzo zwięzłe i ogólne sformułowanie: „znajdź puste pole we fragmencie, które możesz wypełnić zgodnie z Zasadą”; zauważmy, że kolejność kroków tego algorytmu może nie być ustalona na sztywno, np. w przykładzie powyżej można zmienić kolejność dwóch pierwszych kroków, dwóch następnych i trzech ostatnich, zatem to postępowanie algorytmiczne ma ogólniejszą postać niż algorytm ze sztywno zapisaną kolejnością kroków;
- przechodząc od Sudoku w postaci kwadratów łacińskich, przez Sudoku o rozmiarach 4×4 do klasycznego Sudoku, dzieci uogólniają swoje rozumowanie i działania;
- dzieci łatwo przenoszą się na kolejne Sudoku z różnymi rodzajami elementów i na Sudoku o różnych rozmiarach, czyli nie jest ważny charakter elementów tylko, czy ich układ ma własność Sudoku – myślą więc abstrakcyjnie o rozwiązywanej sytuacji;
- dzieci sprawdzają poprawność rozwiązania w trakcie jego otrzymywania lub po uzyskaniu końcowej postaci (pełność i poprawność rozwiązania jest oznaczana po prawej stronie ekranu) i potrafią naprawiać pojawiające się błędy;
- przejawiają przy tym logiczne myślenie w stosowaniu Zasady do różnych rodzajów i rozmiarów Sudoku, budowania algorytmu rozwiązywania i kontroli poprawności tworzonego rozwiązania.
Wyróżnione pogrubioną czcionką terminy, to metody rozumowania (ang. mental tools), składające się na myślenie komputacyjne, które można określić jako zestaw postaw i umiejętności, wzorców myślenia i procesów przydatnych w rozwiązywaniu problemów.
Powyższe punkty można podsumować jednym stwierdzeniem:
Rozwiązując Sudoku, dziecko myśląc logicznie (6), w kolejnych krokach (2) wyszukuje fragmenty (1), które potrafi wypełnić (2), dbając przy tym o spełnienie warunku Sudoku (5), bez względu na charakter elementów (4) i wielkość planszy (3).
Te metody rozumowania można krótko scharakteryzować jako:
- Myślenie logiczne. Myślenie, wyciąganie wniosków i podejmowanie decyzji na podstawie obserwacji, zebranych danych, poznanych faktów i dotychczasowej wiedzy.
- Abstrakcja. Identyfikowanie najważniejszych aspektów problemu, a zaniedbywanie mniej istotnych szczegółów, mających drugorzędne znaczenie dla problemu i procesu jego rozwiązywania.
- Rozkład. Rozkład problemu na mniejsze, łatwiejsze do rozwiązania podproblemy, i skupienie na nich uwagi.
- Projektowanie algorytmu. Budowanie procesu rozwiązywania problemu krok po kroku.
- Uogólnianie. Stosowanie i poszerzenie poznanych rozwiązań do ogólniejszych, zwykle podobnych, problemów.
- Ewaluacja. Ocenianie poprawności i jakości rozwiązań oraz sposobów ich otrzymywania. Może także dotyczyć oceny efektywności procesu rozwiązywania pod względem czasu i przestrzeni w jego przebiegu, w wykonaniu bez komputera i na komputerze.
Sposób rozumowania dzieci podczas rozwiązywania łamigłówek Sudoku odnieśliśmy do sposobów rozumowania, które składają się na myślenie komputacyjne, jedno z najważniejszych podejść do rozwiązywania problemów.
[artykuł: https://www.edu-akcja.pl/publikacje/artykuly/dzieci-przedszkolne/jak-mysla-dzieci-one-mysla-komputacyjnie/]
